Mám pocit, že jsem asi změnil matematiku. To, co mě léta učili, prostě a jednoduše neplatí. Alespoň podle mého počítače. Spustil jsem Microsoft Excel, výborný pomocník pro tabulkové výpočty, vybavený obrovskou spoustou funkcí, které usnadní život. A podívejte, co se stalo.
Zadal jsem do buňky velmi jednoduchý výpočet:

Již děti na prvním stupni základní školy by zvládly tento výpočet vyčíslit – bez počítače, bez kalkulačky. Každý ví, že výsledkem je číslo 0,9. Počítač byl ovšem jiného názoru. Dle jeho propočtů tento výraz dá hodnotu 0,899999999999999. Od té správné se liší pouze o 0,000000000000001. Kdyby takové číslo představovalo délku v metrech, pak by se jednalo přibližně o rozměr atomového jádra. Je to neskutečně malé číslo, fyzikálně zcela zanedbatelné. Ale nikoli matematicky.
Matematika je přesná věda a navíc tento výpočet, jak jsme snadno zjistili se znalostmi základní školy, dává naprosto přesné číslo. Proč tedy počítač lže a říká nám něco jiného?
(Nejnovější verze Excelu se už přibližují lidem a výsledek pro ně správně „zaokrouhlí“.)
Další pokus, opět špatně
Zkusil jsem jít o úroveň výše a začal jsem programovat. Napsal jsem si následující zdrojový kód.

Vy, kteří neumíte programovat, se tím vůbec nemusíte trápit. Program nedělá nic jiného, než se do proměnné pro reálná čísla (pojmenovaná přihrádka v paměti počítače) uloží následující matematický výraz: 0,1 – 0,04 – 0,06. A výsledek vytiskne na obrazovku.
Opět nemusíme znát více, než učí první stupeň základní školy. Výsledkem má být krásná a čistá nula. Ale počítač se se mnou opět chce hádat. Jeho míněním je, že výsledkem je šílené číslo 6.938893903907228E-18. Číslo ještě menší než v prvním příkladu.
Jestliže jsem chybu před tím přirovnával k rozměrům atomového jádra, nyní by snad byly adekvátním příměrem subatomární částice. Ale ať je chyba sebemenší, je tam. Proč moderní a sofistikovaný stroj, jakým počítač je, dělá tak banální chyby? Proč neumí přesně spočítat to, co lecjaký třeťák zvládne s rukama v kapsách?
Odpověď je prostá – tyto chyby vychází z reprezentace čísel v počítači.
V předchozím článku jsme se zabývali celými čísly a jejich reprezentací v počítači. Tento článek nám pomůže pochopit, jak jsou v počítači uložena desetinná čísla. A začneme opět u číselných soustav, kde popsané problémy začínají.
Naše číselná soustava je desítková soustava
Desetinná čísla kromě celé části obsahují ještě část, která je pouze zlomkem celku. Díky těmto číslům můžeme v matematice vyjádřit mnohem bohatší množinu skutečností. Ale desetinná čísla jsou běžně využívána i v běžné, nematematické praxi. Člověk měří přibližně 1,8 metru. Byt stojí 2,7 milionu korun. Délka výrobku je 0,713 metru.
Pojďme poslední číslo prozkoumat trochu podrobněji. Jak vznikne? Každé desetinné číslo můžeme popsat následujícím způsobem:

Naše číslo 0,713 tedy můžeme zapsat takto:

Vše funguje v podstatě stejně jako u celých čísel. Není také žádného důvodu k tomu, aby tomu tak nebylo. Čísla, která mají nenulovou celou část, pak budou obsahovat jak členy se zápornými mocninami desítky, tak členy s kladnými mocninami desítky. Číslo 26,814 bychom mohli zapsat takto:

Jediné, co jsme udělali, je to, že jsme rozšířili princip platný pro celá čísla za desetinnou čárku. Postupujeme stejně, pouze využíváme mocniny desítky se záporným exponentem.
Číselná soustava počítače – dvojková soustava
Přesuneme se plynule do soustavy, která je vlastní počítačům. Jak vypadá desetinné číslo ve dvojkové soustavě? Lze říci, že jeho vyjádření je analogií vyjádření desetinného čísla v desítkové soustavě. Pochopitelně pracujeme s mocninami o základu 2.
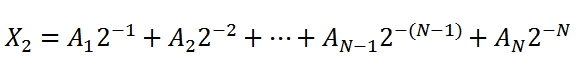
Takže třeba toto číslo

představuje v klasické desítkové soustavě číslo 0,8125. Jak jsme k němu došli? Vyčíslili jsme uvedený výraz (1 × 0,5 + 1 × 0,25 + 0 × 0,125 + 1 × 0,0625).
Převod mezi různými soustavami
Dostáváme se k vysvětlení problémů popsaných na počátku tohoto článku. Pokud má fungovat komunikace mezi počítačem a člověkem, musí být možné jednoznačně a úplně převádět čísla z jedné soustavy do druhé a zpět.
V článku o celých číslech jsme si ukázali, že u nich problém není. Ale jak je to s čísly desetinnými? Postup, kdy nás zajímá konkrétní převod z desítkové soustavy do dvojkové, je následující: Číslo opakovaně násobíme dvojkou a zapisujeme výsledek celou část výsledku s tím, že zbytek pokračuje ve výpočtu. Celá část logicky může být jednička či nula. Ukážeme si to na příkladu – budeme chtít do dvojkové soustavy převést číslo 0,3.

Mohli pokračovat do nekonečna. Výsledkem je tedy číslo zapsané periodickým rozvojem – číslo 0,01001, přičemž část 1001 se opakuje do nekonečna.
V této podobě se ještě stále nic brutálního neděje. Je sice zajímavé, že číslo, které je v jedné číselné soustavě vyjádřeno bez period, s konečným počtem číslic, a ve druhé je zapsáno jako číslo s nekonečným periodickým rozvojem, ale stále není důvod panikařit. Tento důvod nastane, jakmile začneme číslo reálně ukládat v počítači. Tam je totiž místo pro ukládání čísel omezené. A nekonečný desetinný rozvoj prostě do konečného prostoru nelze uložit. Nedá se uložit ani přímo periodická část.
Jedinou možností, kterou máme, je uložit pouze omezený počet číslic. Tím ovšem vznikne nepatrný rozdíl mezi tím, jaké číslo bude uloženo, a tím, jaké číslo jsme ve skutečnosti chtěli uložit. Podívejme se na příklad. Představme si, že můžeme uložit pouze osm platných číslic. Naše číslo tedy bude vypadat takto:
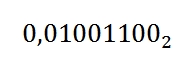
Když tímto způsobem uvedené číslo převedeme do desítkové soustavy, dostaneme následující výsledek.

My jsme ale původně chtěli uložit číslo 0,3. Tímto zaokrouhlením binárně vyjádřeného čísla jsme uložili číslo, které je o 0,003125 menší. Tento rozdíl sice vypadá jako malý, ale hlavní problém spočívá v tom, že počítač principiálně ukládá nepřesná čísla.
Není to chybný stav, je to vlastnost, která vyplývá přímo z konstrukce počítačů. Kdybychom zvolili číslo s větší přesností, pak bude rozdíl mnohonásobně menší, ale principiálně bude generován zcela totožně.
Obecně totiž neplatí, že by existoval jednoduchý způsob převodu čísla z desítkové soustavy do dvojkové soustavy tak, aby bylo možné tuto transformaci obrátit s nezměněným výsledkem. To je důvod, proč jsme v příkladech na začátku kapitoly dostali nepřesné výsledky. Není to kvůli tomu, že by počítač špatně počítal. Je to proto, že počítač počítá se špatnými čísly, neboť ta správná nedokáže zcela přesně uložit.
Důsledky a řešení
Důsledky jsou jednoznačné. Počítač nepočítá zcela správně. To, nač byl počítač primárně určen, nezvládá zcela dokonale. Na jednoduchých příkladech jsme viděli, jaké jsou důsledky. Drobná chyba se navíc dále přenáší do výpočtu jako celku a může nakonec nabývat ohromujících rozměrů.
Mnohé tyto chyby však lze odstranit tím, že vhodně uspořádáme výpočet, že vhodně budeme pracovat se samotným ukládáním čísel. To je důvod, proč se dnes tyto chyby reálně projeví jen ve vzácných případech podobných těm, které jsme si zde ukázali.
