Webové mapy nám děsně lžou. Skutečnost vypadá úplně jinak a řekneme vám proč

Grónsko je sice největší ostrov na světě, ve srovnání s africkým kontinentem je ale 14× menší. Jak je tedy možné, že na většině webových map vypadá spíše jako další zamrzlý kontinent a skoro větší než zmíněná Afrika?

Odpověď je vlastně docela jednoduchá. Byť dnešní webové mapy nabízejí neuvěřitelný detail a přiblížení, jakmile je oddálíte na celé kontinenty, projeví se jejich principiální geometrický neduh. Odjakživa nám tak trochu lžou, a je to úplně normální.

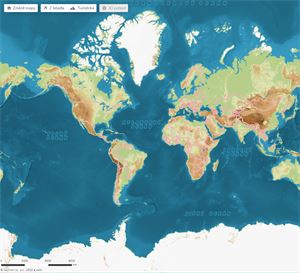
Ne, takhle svět ve skutečnosti nevypadá (Mapy.cz)

Arktické Česko by bylo velké jako Německo

A jelikož si na to od dob školního zeměpisu už často nepamatujeme, s otevřenou pusou pak zíráme na weby jako The True Size a Country Centered Map Projections, které ukážou velikost libovolného území podle toho, do jaké zeměpisné šířky jej posuneme.

12 netradičních map České republiky, které jste ještě nikdy neviděli

Když Česko přemístíte vysoko nad Skandinávii, rázem bude zdánlivě větší než Německo. A když ho naopak ponížíte k rovníku, smrskne se na úroveň Moravy.

Klam mapových projekcí, aneb Česko v různých zeměpisných šířkách

Jak je to možné? Vše plyne z jedné geometrické nepříjemnosti. Země bohužel nemá tvar žehlícího prkna. Není to rovina, ale všemožně zprohýbaný kulovitý geoid, který musíme nějakým způsobem do roviny teprve promítnout. A to je bez deformace ploch, délek nebo úhlů zhola nemožné.

Do další části – klikněte na šipku – jsme připravili dvě jednoduché, ale často používané projekce. Názorně uvidíte, v čem je problém.

Promítneme body ze středu

Pojďme si vyzkoušet zobrazení na dokonalé kouli, kterou bychom chtěli promítnout na válec. Právě válcové zobrazení je dnes ostatně to zdaleka nejrozšířenější a používají jej i všechny zmíněné všeobecné mapové služby na webu.

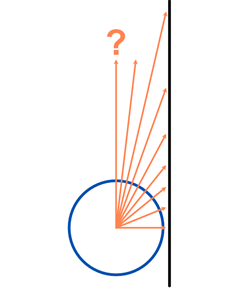
Promítnutí všech bodů na válec prostým protažením od středu

Povrch koule bychom mohli promítnout jako na obrázku výše. Stěna válce se koule dotýká na rovníku, no a my všechna ostatní místa jednoduše protáhneme od středu pod stejným úhlem, dokud se nám nestřetnou se stěnou válce.

Má to jeden háček. Čím více se budeme blížit k pólům, tím se nám budou body na válci promítat ve větší vzdálenosti a póly samotné se s válcem střetnou nekonečně daleko – nikdy.

Promítneme body vodorovně

Co s tím? Místo toho bychom mohli body na povrchu koule promítnout vodorovně. Projekce bude opět nejvěrnější na rovníku, kde se válec dotýká koule, a získáme i polární oblasti, jenže ty se nám tentokrát naopak smrsknou do úzkého proužku.

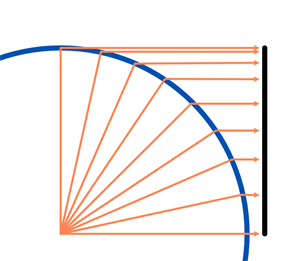
Promítnutí všech bodů na kouli vodorovně

Míru zkreslení názorně vyjadřuje tzv. Tissotova indikatrix. V další části vysvětlíme, o co jde.

Tissotova indikatrix

Ať si vyberete jakýkoliv způsob projekce, vždy budete muset zaplatit nějakou daň, která se bude odvíjet od toho, v jakém místě protneme kouli s rovinou. Tam bude deformace vždy nejmenší.

Míru lokálního zkreslení celkem názorně vyjadřuje třeba tzv. Tissotova indikatrix. Je to soustava elips nad projekcí, jejichž tvar odpovídá i způsobu deformace. Kdyby měly elipsy ve všech místech mapy stejný tvar, zobrazení bude prakticky dokonale odpovídat originálu. Tomu se přibližuje třeba klasický glóbus.

Míra zkreslení v první a druhé válcové projekci

Tissotova indikatrix pro naše dvě primitivní válcové projekce potvrzuje to, co bylo patrné už z řezů. U prvního příkladu se nám elipsy směrem od rovníku zvětšují – u toho druhého zase zplošťují.

Přesnější neznamená automaticky praktičtější

Mohlo by se zdát, že nejlepší mapou bude ta, kde bude indikatrix ve všech bodech stejná, anebo bude docházet k deformacím třeba jen kdesi uprostřed Pacifiku, kde není nic zajímavého, a tak nás to nebude trápit, stejně jako nás netrápí absurdní tvar Antarktidy na běžných mapách.

Takové projekce sice existují, ovšem za cenu atypických orientací. Třeba polární zobrazení Charlese Sanderse Peirceho z konce 19. století, ve kterém má rovník tvar čtverce a Antarktida je rozřezaná do všech mapových rohů.

Atypické zobrazení má nad kontinenty relativně nízké vzájemné zkreslení

Obydlené kontinenty sice trpí relativně nízkým vzájemným zkreslením, protože deformace se soustředí nad oceány. Takto by ale Mapy.cz vypadaly asi jen v nějakém paralelním vesmíru, ve kterém namísto rodu Homo zvítězil Ursus maritimus.

Problém v 16. století částečně vyřešil Gerhard Mercator. Jeho zobrazení dnes používají třeba mapy od Googlu. Povíme si o něm v další části.

Úhlojevná mapa pro mořeplavce

Nakonec vše dopadlo úplně jinak. Roku 1569 se totiž jistý vlámský kartograf Gerhard Mercator pochlubil válcovým zobrazením, které vychází z prvního příkladu.

Tento způsob projekce se vzájemně pravoúhlými poledníky a rovnoběžkami totiž nabízí jednu nesmírnou výhodu. Sice deformuje plochy, nikoliv ale úhly. Proto mu říkáme úhlojevné – konformní zobrazení.

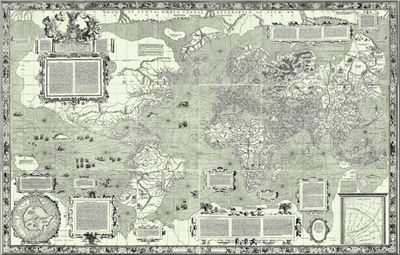
Mercatorova mapa z roku 1569

Jednoduše řečeno: křivka spojující dvě místa na mapě, která protíná poledníky pod stejným úhlem, má tvar přímky. Mořeplavec pozdního novověku tedy na podobné mapě jen spojil dvě místa úsečkou – říkáme ji loxodroma –, odečetl úhel a věděl, že když se bude setrvale držet kurzu, dopluje do cíle.

Loxodroma nemusí odpovídat ortodromě – nejkratší spojnici dvou bodů na zemském povrchu. Nicméně díky úhlojevným mapám umožnila snadnou plavbu na velké vzdálenosti a stala se základem moderních námořních tras. 

Webový Mercator

Mercatorovo zobrazení a jeho moderní odnože sice výrazně deformují severní a jižní oblasti planety, přesto v různých variantách sloužily celá další staletí. Význam válcové úhlojevné mapy nakonec ještě vzrostl s nástupem letecké dopravy ve 20. století a na její webové variantě svoji projekci postavil i Google a ostatní globální hráči.

Webový Mercator je synonymem digitální mapy světa

Deformace severních a jižních zeměpisných šířek je v tomto případě o něco málo slabší než v čistě válcovém zobrazení. Grónsko, Kanada, Skandinávie, a zvláště Rusko jsou však i tak výrazně větší než ve skutečnosti.

V poslední části zmíníme ještě projekci Gall-Peters a jedno dokonalé, jednoduché řešení 

Plochojevný, tedy politicky korektní

Druhá polovina 20. století a výpočetní techniky usnadnily rozvoj nových typů zobrazení, které dnes bojují o své místo pod sluncem.

Jedním z těch nejcitovanějších je válcová plochojevná projekce Gall-Peters, která protíná planetu na 45 stupni severní i jižní zeměpisné šířky a v těchto místech tedy nedochází k žádné destrukci. 

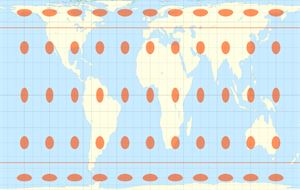
Míra zkreslení projekce Gall-Peters

Podstatu plochojevné projekce vystihuje Tissotova indikatrix výše. Sice dochází ke zkreslení úhlů a délek, nikoliv však ploch – jejich výměr. Tvar elips se sice dle zeměpisné šířky mění, jejich obsah je ale stále stejný.

Gall-Peters by tedy měl podle svých propagátorů podávat lepší představu o vzájemné velikosti jednotlivých kontinentů, oproti Mercatorovi se nám totiž zploštily severní a jižní okraje (vzpomeňte si na náš druhý příklad projekce z úvodu článku). Rusko už není tak děsivé, Afrika je obrovská a Grónsko patřičně titěrné.

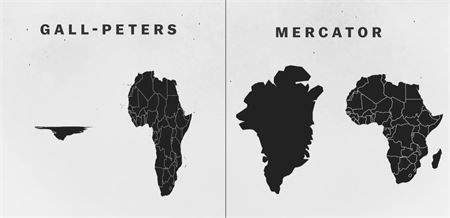
Gall-Peters, Mercator a (nejen) grónský paradox 

A proč prostě nepoužít glóbus?

Gall-Peters může dobře sloužit na nástěnných mapách a ve školních atlasech, ještě lépe ale poslouží starý dobrý glóbus a dynamická projekce, která se mění jednoduše podle měřítka. Díky ohromnému výpočetnímu výkonu našich počítačů může Země na monitoru počítače a v globálním měřítku opět vypadat tak, jak má. Jako koule. Stačí spustit webový Google Earth.

Grónsko i Afrika ve správných poměrech

Když Earth přiblížíte, zobrazí se některá z hromady projekcí, jejichž deformace na místní úrovni je už natolik nízká, že ji okem stejně nepostřehnete.